Освойте расчет средневзвешенного значения в Excel! В этой статье вы найдете:
- Подробные инструкции по расчету средневзвешенного значения.
- Пошаговое руководство с примерами.
- Формулы для разных случаев.
В руководстве демонстрируются два простых способа расчета средневзвешенного значения в Excel — с помощью функции СУММ или СУММПРОИЗВ, а также при помощи сводной таблицы.
В одной из предыдущих статей мы обсудили основные функции для того, чтобы вычислить среднее значение в Excel, которые очень просты и просты в использовании.
Когда вы рассчитываете среднее значение для набора значений, вы обычно работаете со значениями, имеющими одинаковый вес и важность.
Но что, если некоторые значения имеют больший «вес», чем другие, и, следовательно, вносят больший вклад в итоговое среднее значение? В таких ситуациях вам необходимо рассчитать средневзвешенное значение.
В этой статье мы расскажем, как использовать создать формулу средневзвешенного значения в Excel, а также приведем несколько примеров.
Формула средневзвешенного значения — это инструмент, используемый для расчета средних значений, взвешенных по разным весам или другим значениям. Другими словами, каждому усредняемому значению присваивается определенный вес.
Хотя Microsoft Excel не предоставляет специальной функции чтобы посчитать средневзвешенное значение, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что и показано в следующих примерах.
Что такое средневзвешенное значение?
Средневзвешенное значение — это своего рода среднее арифметическое, в котором некоторые элементы набора данных имеют большее значение, чем другие.
В бизнесе средневзвешенное значение часто используется в таких задачах, как:
- оценка портфеля акций, когда у каждой из них своя ценность/рисковость
- оценка прогресса по проекту, когда у задач не равный вес и важность
- оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
Например, оценки учащихся часто рассчитываются с использованием средневзвешенного значения, как будет рассмотрено ниже. Обычное среднее значение легко вычисляется с помощью функции Excel СРЗНАЧ. Но во многих случаях простое среднее нас не устроит.
Если мы будем говорить о подготовке специалиста определенной квалификации и специализации, то некоторые дисциплины и умения однозначно будут более важными. К примеру, нас интересуют те, кто лучше подготовлен к работе в Excel и к программированию. С этой точки зрения каждой дисциплине мы присвоим определенный вес с учетом ее значимости для подготовки нужного нам специалиста.
То есть мы хотим, чтобы формула средней оценки учитывала важность, или вес каждой изученной учебной дисциплины. Ниже мы рассмотрим это на примерах.
Методы расчета будут зависеть от имеющихся исходных данных.
Формулы для средневзвешенного значения в Excel
В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.
Пример 1. Сумма весов равна 100%
Предположим, у вас есть набор данных с оценками, полученными студентом на разных экзаменах, а также весами в процентах.
Учащийся получает оценки по разным учебным дисциплинам, но в результате ему необходимо поставить итоговый балл. Здесь некорректно рассчитать простое среднее значение, поскольку важность различных дисциплин различается.
Например, информатика с весом 30% имеет 6 раз больший вес по сравнению с пением и рисованием, у которых вес только 5%.
Чтобы с точки зрения математики получить средневзвешенное значение итоговой оценки, нужно перемножить все оценки на их веса и полученные результаты сложить.
9*30%+6*10%+8*10%+10*30%+6*5%+4*5%+5*5%+6*5%=8.15
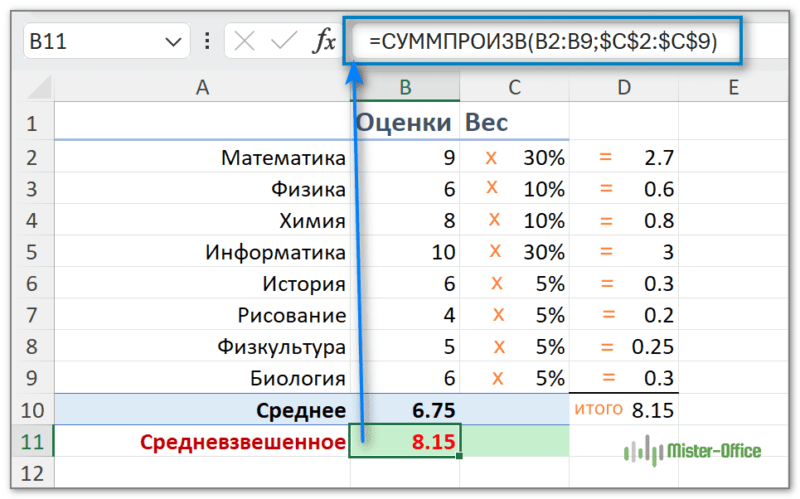
Если у вас есть базовые знания о функции СУММ, приведенная ниже формула вряд ли потребует какого-либо объяснения:
=СУММ(B2*C2; B3*C3; B4*C4; B5*C5; B6*C6; B7*C7; B8*C8; B9*C9)
По сути, здесь мы выполняем те же вычисления, что и были описаны выше, за исключением того, что вместо чисел вы указываете ссылки на ячейки.
Продолжая использовать тот же набор данных, вот короткая формула, которая даст вам средневзвешенное значение с помощью функции СУММ:
=СУММ(B2:B9*C2:C9)
Хитрость при использовании этой формулы заключается в том, чтобы при ее вводе использовать CTRL + Shift + Enter, а не просто Enter. Поскольку функция СУММ не может обрабатывать массивы, вам необходимо использовать CTRL + Shift + Enter.
При этом обязательно убедитесь, что сумма весов равна 100%. Если это не так, вам нужно разделить результат на сумму весов (как показано в примерах ниже).
Хотя формула СУММ очень проста и понятна, она не является подходящим вариантом, если вам нужно посчитать средневзвешенное от большого количества значений. Да и формулу массива вводить не слишком удобно.
Если у нас для каждого элемента имеется свой вес в процентах, и сумма этих весов равна 100%, гораздо проще вместо функции СУММ использовать функцию СУММПРОИЗВ, чтобы получить средневзвешенное значение всех оценок.
Вот формула, которая даст вам средневзвешенное значение в Excel для нашего примера:
=СУММПРОИЗВ(B2:B9;C2:C9)
Функция СУММПРОИЗВ Excel идеально подходит для этой задачи, поскольку она как раз и предназначена для суммирования произведений, а это именно то, что нам нужно. Таким образом, вместо того, чтобы умножать каждое значение на его вес по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом случае массив представляет собой непрерывный диапазон ячеек):
=СУММПРОИЗВ( диапазон_значений ; диапазон_весов )
Вот как работает эта формула : Функция Excel СУММПРОИЗВ умножает первый элемент первого массива на первый элемент второго массива. Затем она умножает второй элемент первого массива на второй элемент второго массива. И так далее..
И, наконец, она складывает все эти значения.
Как видите, полученный средневзвешенный балл, как бы мы его не рассчитывали, значительно отличается от обычной средней оценки, когда мы просто сложили все значения и разделили на их общее количество.
Пример 2. Когда сумма весов не равна 100 %
В приведенном выше случае веса были присвоены таким образом, чтобы общая сумма составляла 100%. Но в реальных жизненных ситуациях это не всегда так.
Давайте посмотрим пример с разными весами.
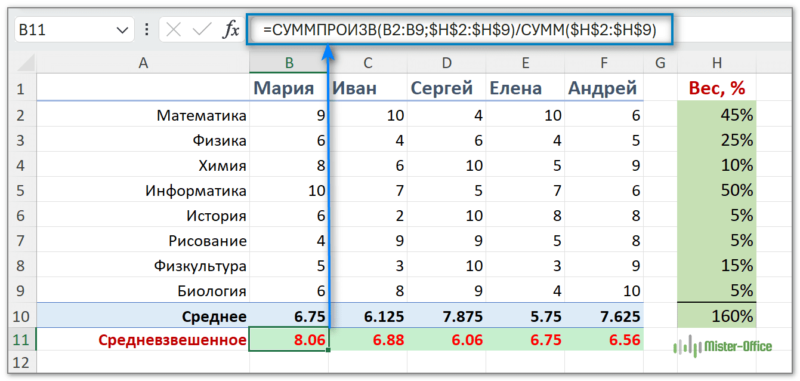
В приведенном выше случае сумма весов составляет 160%.
Если использовать формулу СУММПРОИЗВ из предыдущего раздела, она даст неверный результат.
Вот формула, которая позволит посчитать средневзвешенное с любыми весами значений:
=СУММПРОИЗВ(B2:B9;$H$2:$H$9)/СУММ($H$2:$H$9)
То есть, необходимо сумму произведений значений и весов разделить на сумму весов.
= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )
А теперь рассмотрим пример расчета средневзвешенного значения, когда нет никаких весов, а их нужно рассчитать.
Пример 3. Когда необходимо рассчитать веса
Как мы уже выяснили, при использовании функции СУММ или СУММПРОИЗВ для нахождения средневзвешенного значения в Excel сумма весов необязательно должна составлять 100%. Их также необязательно выражать в процентах.
Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:
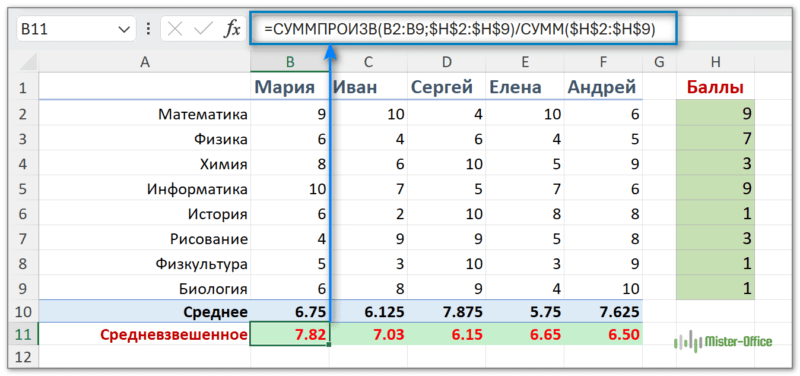
Обратите внимание, формула расчета здесь та же, что и в предыдущем примере:
=СУММПРОИЗВ(B2:B9;$H$2:$H$9)/СУММ($H$2:$H$9)
Видите, в этом случае мы обошлись без процентов.
Пример 4. Расчет средневзвешенной цены товара.
По такому же принципу мы можем рассчитать и средневзвешенную цену товара.
Обычно при подажах мы имеем разные цены для разных покупателей. Вес и значимость конкретной цены будет определяться объемом продаж. Чем больше продано товара по определенной цене, тем более значима эта цена и тем больше будет ее вклад в формирование средневзвешенной цены продажи товара.
Вто формула средневзвешенной цены для нашего условного примера:
=СУММПРОИЗВ(B2:B6;C2:C6)/СУММ(C2:C6)
Результат расчета вы видите на скриншоте ниже.
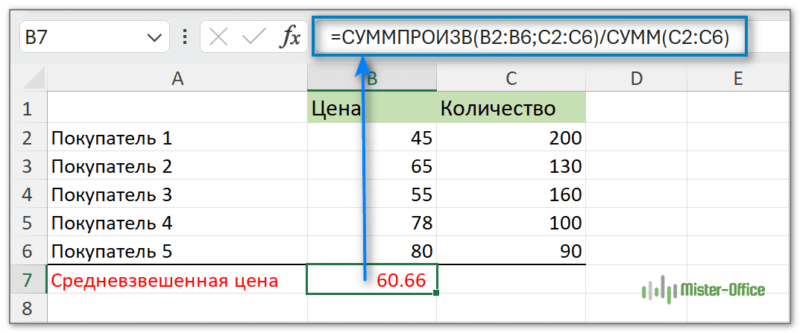
Разделив результат СУММПРОИЗВ на СУММ количеств, можно гарантировать, что сумма весов (в данном случае количеств) составит 100%.
Расчет средневзвешенной цены в сводной таблице
Как мы уже убедились, средневзвешенное значение легко вычислить при помощи функций СУММПРОИЗВ и СУММ. Однако, если у нас есть большой объем информации о продажах различных товаров, имеет смысл попробовать использовать для расчетов сводную таблицу.
Давайте рассмотрим пример, как при помощи сводной таблицы мы можем рассчитать средневзвешенную цену сразу по всем имеющимся товарам. Думаю, это значительно удобнее, нежели составлять отдельный расчет по каждому товару, как мы делали это выше.
Итак, рассмотрим условный пример с такими данными о продажах:
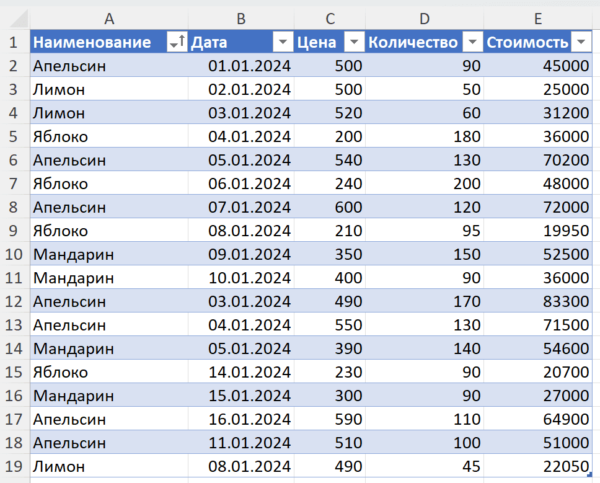
Попробуем рассчитать средневзвешенную цену по всем перечисленным в этой таблице товарам.
Создадим сводную таблицу. Вы можете воспользоваться этим руководством: Как сделать сводную таблицу – пошаговая инструкция.
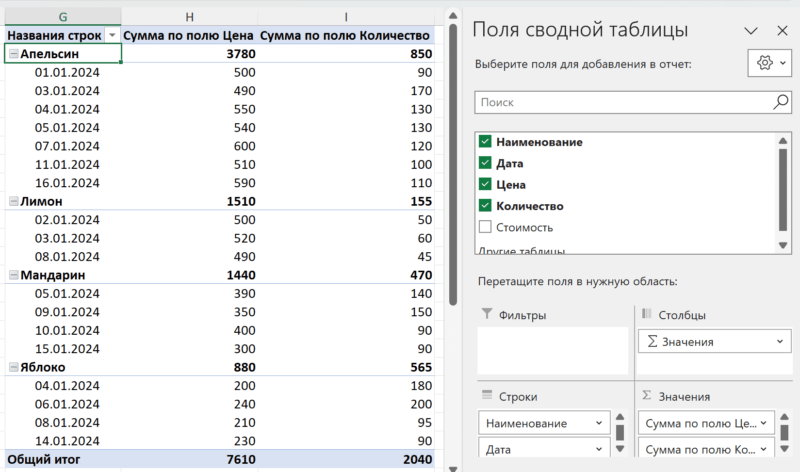
На итоговые значения по полю «Цена» не обращайте внимания, так как простое арифметическое сложение цен не имеет экономического смысла.
Давайте добавим вычисления в нашу таблицу.
К сожалению, вычисляемые поля в сводной таблице не поддерживают функции Excel такие как СУММПРОИЗВ и СУММ. Поэтому мы не сможем использовать формулы, рекомендованные в предыдущих разделах. Но все же решение есть.
Выберите любую ячейку в сводной таблице, чтобы активировать на ленте меню Анализ сводной таблицы.
Выберите пункт Поля, элементы и наборы – Вычисляемое поле. Создайте новое вычисляемое поле, которое можно назвать «Средняя цена». Создайте формулу для этого поля, выбирая имеющиеся поля сводной таблицы и используя математические знаки.
Вы можете это видеть на скриншоте ниже.
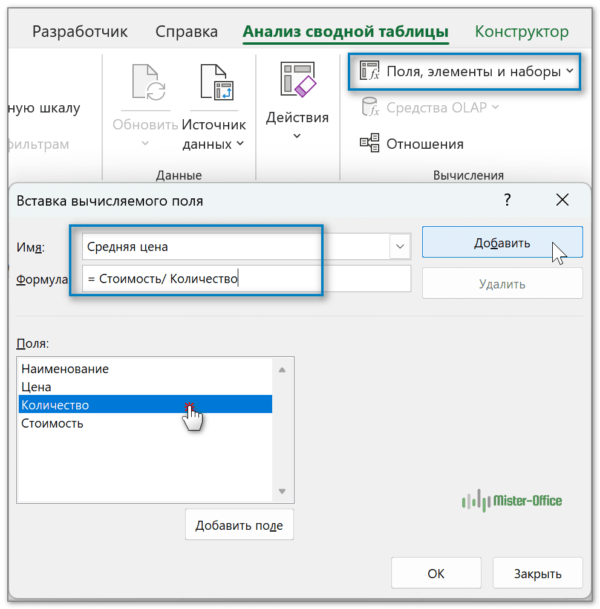
Записав таким образом формулу вычисляемого поля, нажмите кнопку «ОК».
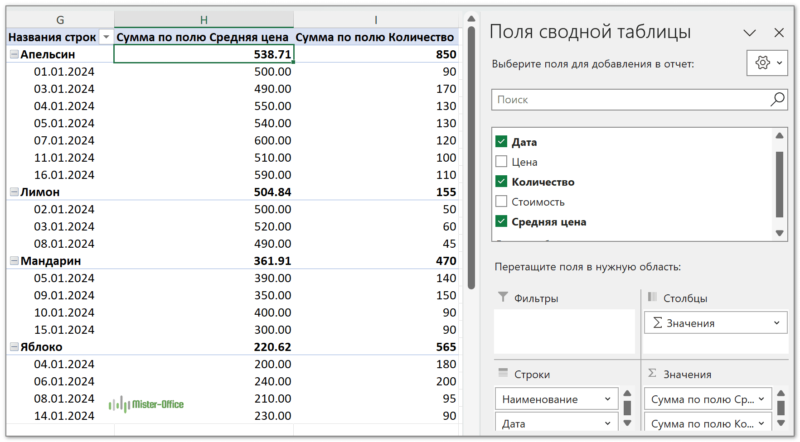
Теперь вернемся к сводной таблице и добавим поле Средняя цена в область значений. Как видно на скриншоте ниже, в строке итогов по каждому товару можно увидеть его средневзвешенную цену, а ниже в этом столбце – реальные цены продаж, из которых эта средневзвешенная цена сложилась.
В следующем столбце вы видите соответствующее каждой цене количество товара, которое как раз и было использовано в качестве весов.
Ну, это все о формуле средневзвешенного значения в Excel.
Как видно из рассмотренных нами примеров, рассчитать средневзвешенное значение в Excel несложно, если следовать описанным выше шагам. Этот метод можно применять в различных ситуациях, когда важно учитывать вес каждого значения при расчетах.
Таким образом, умение рассчитывать средневзвешенное значение в Excel – это важный навык для анализа данных, который поможет вам принимать обоснованные решения на основе ваших данных. Воспользуйтесь этой информацией и улучшите свои навыки работы с Excel!